Num tempo em que alguns políticos tentam modificar ou dourar a verdade, fazendo-nos crer que o branco é preto ou que o calor é frio, o pensamento crítico e racional, além de fundamental, é absolutamente sinónimo da liberdade que merecemos.

Mas, tal como acontece nos dias de hoje, a arrogância, aliada à ignorância e estupidez, são os ingredientes para a falta de racionalidade na tomada de decisões que influenciam as sociedades e os seus cidadãos.

De que falo?

De uma insubstituível banalidade que se comemora no dia de hoje – um número, uma constante matemática, mais concretamente, a razão que existe entre o perímetro de uma circunferência e o seu raio, de seu nome π (a letra minúscula grega) ou pi, ou seja, π = perímetro/ diâmetro.

Esta razão é constante para círculos de qualquer tamanho, ou seja, é uma constante universal, e como tal não passível de discussão, simplificação ou modificação, ao contrário de formas de vermos o mundo ou mesmo os outros, passíveis de discussão ou de maneiras diferentes de serem encaradas, dentro do respeito e tolerância pelas ideias diferentes.

Ora do que falo é a tentativa de legislar sobre a constante matemática pi, que ocorreu no final do século XIX (1897),no estado norte-americano do Indiana. Isso aconteceu pela mão do médico e matemático amador Edward Goodwin, autor de um projeto de lei que pretendia legislar sobre constantes e verdades matemáticas.

E quais foram os seus principais erros?

Apenas no cálculo da área do círculo, já que pretendia que o Pi fosse arredondado para 3.2, quando, de há séculos, se sabe que esta constante é infinita e não periódica, com um valor aproximado à quinta casa de 3.14159.

O raciocínio do Dr. Goodwin, entre muitos outros erros, estipulava que ele haveria descoberto a solução ao velho problema da “quadratura do círculo”, ou seja, de que seria possível construir um quadrado com a mesma área de de um determinado círculo apenas usando uma régua e um compasso.

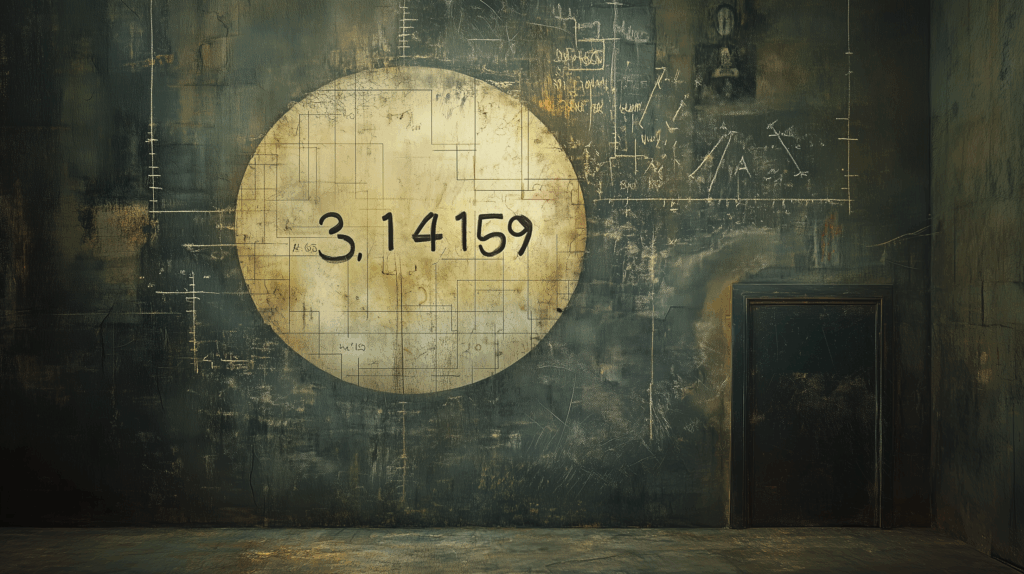
Ora este problema, que atraía muitos matemáticos amadores daqueles tempos, já havia sido demonstrado como sendo de impossível resolução.

Em 1882, Ferdinand von Lindemann tinha provado de forma rigorosa que Pi é um número transcendente (ou número não algébrico), o que implica que não pode existir uma quadratura perfeita do círculo com compasso e reta.

Regressando ao médico amador Dr. Goodwin e à sua proposta legislativa de arredondar o Pi para 3.2.

Quais teriam sido as consequências nos dias de hoje desse delírio político, caso o estado de Indiana, e em sequência, no resto do mundo?

Os campos do dia-a-dia atual afetados pelo tal arredondamento legislativo de Pi seriam quase inumeráveis, mas destaco apenas alguns mais facilmente percetíveis:

Medicina

Um robô cirúrgico realizando uma operação delicada:

• Cálculos de trajetória e velocidade dependem de π.
• Com π = 3,14159: conforme programado.
• Com π = 3,2: Erro de posicionamento de aproximadamente 1,9%.

Circuitos Elétricos em Ressonância (pacemaker)

Um pacemaker utiliza circuitos LC (indutor-capacitor) o que envolve uma fórmula onde entra o π.

• Com π = 3,14159: Frequência precisa e estimulação cardíaca adequada.
• Com π = 3,2: O pacemaker estimularia o coração a aproximadamente 98,2% da frequência pretendida.

Para um paciente programado para 60 batimentos por minuto, o coração bateria a 58,9 batimentos por minuto, diferença que, acumulada durante largos períodos, poderia originar fadiga crónica, uma menor capacidade física e eventuais complicações cardíacas.

Equipamento de Ressonância Magnética num hospital:

estes equipamentos de imagiologia médica utilizam equações com π para reconstruir imagens a partir de sinais de radiofrequência.

• Com π = 3,14159: Imagens precisas dos órgãos e dos tecidos.
• Com π = 3,2: Distorções sistemáticas nas imagens sem qualquer valor diagnóstico.

Um tumor cerebral de 5 mm poderia aparecer com 5,1 mm e numa posição ligeiramente diferente, alterando potencialmente as decisões cirúrgicas e aumentando o risco para o paciente.

 Ecrãs táteis (telemóveis e tablets, por ex.)

As telas sensíveis ao toque calibram os campos elétricos em padrões circulares:

• Com π = 3,14159: Deteção precisa do toque.
• Com π = 3,2: Erro de deteção aumentando nas extremidades do ecrã.

Ao se digitarem mensagens num smartphone, existiriam mais erros de digitação perto das extremidades do teclado virtual. Por exemplo, aplicações como mapas teriam uma menor precisão durante os habituais gestos de zoom efetuados com os dois dedos.

Medicamentos e Mecânica Quântica

No modelo do átomo de hidrogénio, a função de onda do eletrão depende de π:

• Com π = 3,14159: Previsões precisas sobre propriedades químicas.
• Com π = 3,2: Cálculos de orbitais atómicos alterados levariam a previsões incorretas sobre ligações químicas.

Um medicamento projetado com simulações moleculares usando π = 3,2 teria interações terapêuticas distintas das esperadas, tornando-se ineficaz ou mesmo potencialmente tóxico.

Processamento de Áudio Digital

Num serviço de streaming de música como Spotify:

Os algoritmos de compressão de áudio (MP3, AAC) usam Transformada de Fourier com π.

• Com π = 3,14159: Áudio de alta-fidelidade com compressão eficiente.
• Com π = 3,2: Distorções percetíveis em frequências específicas.

Notar-se-iam artefactos estranhos em notas de piano ou violino, tornando a experiência musical menos agradável. Instrumentos de cordas soariam particularmente “fora de tom”.

Navegação por Satélite (GPS)

O sistema GPS utiliza triangulação baseada em tempo e distância, onde π é decisivo para os cálculos orbitais e do posicionamento.

Navegação marítima num percurso de 1.000 km.

• Com π = 3,14159: Cálculos de rota precisos.
• Com π = 3,2: Erro acumulado de aproximadamente 19 km ao final da viagem.

Um navio poderia encalhar ou colidir com obstáculos devido a esse desvio. Para aviões, um erro similar num voo transatlântico poderia significar aterrar no aeroporto errado ou ficar sem combustível antes de chegar ao destino.

Excerto do Indianapolis Sun: Um Homem de Génio, Mas Algumas Pessoas Não lhe Chamam Isso. O Dr. Goodwin não presta atenção às suas provocações, mas mantém-se próximo do seu trabalho de croché e espera ver o dia em que o mundo acreditará na sua teoria de um quadrado redondo ou do que quer que lhe chamem. (tradução LAR)

Voltando ao Projeto de Lei do Pi, e após ter sido previamente aprovado na Câmara dos Representantes do Estado do Indiana, acontece que, durante a sessão de votação final, a proposta viria a ser chumbada no Senado, graças à intervenção do Professor C. A. Waldo, da Universidade de Purdue, que, por acaso, estava presente na sessão da votação final.

O projeto de lei do Pi tornou-se um exemplo clássico:

– dos perigos de legislar sobre factos científicos ou matemáticos

– da importância da literacia científica entre os legisladores

– do fosso entre o entusiasmo amador e os princípios matemáticos estabelecidos.

Tal como querer coartar a liberdade de cada um, obrigar a que leis naturais ou constantes matemáticas fiquem sujeitas à vontade de um qualquer mortal é impossível. Pelo menos sem consequências. Quer no que diz respeito à liberdade, quer no que envolve constantes físicas ou matemáticas.

Esta história sublinha a necessidade imperiosa de termos pensamento crítico e literacia científica, do simples cálculo às garantias de liberdades e direitos cívicas.

Fonte consultada:

Quem tiver interesse em conhecer mais profundamente esta história, pode consultar gratuitamente
Hallerburg, Arthur E. “House Bill no. 246 revisited.” Proceedings of the Indiana Academy of Science. Vol. 84. 1974. Disponível gratuitamente em: https://journals.indianapolis.iu.edu/index.php/ias/article/view/4753/4589